DAFTAR ISI
1. PENDAHULUAN [Back]
Rangkaian aritmetika adalah blok bangunan fundamental dalam sistem digital. Penjumlahan dan pengurangan adalah dua operasi aritmetika paling dasar. Percobaan ini berfokus pada perancangan rangkaian yang dapat melakukan baik half-addition atau half-subtraction dari dua bilangan biner satu bit, yang dapat dipilih melalui input kontrol. Rangkaian ini, yang dikenal sebagai half-adder/subtractor, mendemonstrasikan bagaimana gerbang logika dapat dikonfigurasi untuk melakukan fungsi aritmetika yang berbeda berdasarkan sinyal kontrol.
2. TUJUAN[Back]
- Merancang rangkaian logika yang mampu melakukan baik half-addition maupun half-subtraction.
- Memahami operasi dari sebuah half-adder dan sebuah half-subtractor.
- Memanfaatkan input kontrol untuk memilih antara operasi penjumlahan dan pengurangan.
- Memverifikasi tabel kebenaran untuk rangkaian half-adder/subtractor.
3. ALAT DAN BAHAN[Back]
ALAT
- Software Proteus 8.17
Proteus Design Suite adalah sebuah paket perangkat lunak (software suite) yang sangat populer dan serbaguna dalam bidang desain dan simulasi elektronik. Secara fundamental, Proteus menawarkan lingkungan terintegrasi untuk mendesain skematik rangkaian elektronik, melakukan simulasi fungsional dari rangkaian tersebut (termasuk simulasi mixed-mode untuk sirkuit analog dan digital), serta merancang layout Papan Sirkuit Tercetak (PCB) yang siap untuk manufaktur. Fitur unggulannya adalah kemampuan Virtual System Modelling (VSM), yang memungkinkan pengguna untuk mensimulasikan mikrokontroler beserta kode firmware-nya secara bersamaan dengan komponen elektronik lainnya, sehingga memungkinkan pengujian dan debugging sistem tertanam (embedded systems) secara virtual sebelum pembuatan prototipe fisik. Dengan perpustakaan komponen yang luas dan alat desain yang intuitif, Proteus menjadi pilihan utama bagi insinyur elektronik, teknisi, maupun pelajar untuk mempercepat proses desain, mengurangi biaya pengembangan, dan meminimalkan kesalahan dalam proyek elektronika.
BAHAN
- LOGICSTATE
Dalam dunia elektronika digital, logic state merujuk pada salah satu dari dua kondisi fundamental yang dapat dimiliki oleh sinyal digital: "tinggi" (high) atau "rendah" (low), yang secara konvensional direpresentasikan sebagai logika '1' dan logika '0'. Kondisi ini diwujudkan dalam level tegangan tertentu dalam sirkuit; misalnya, dalam sistem TTL (Transistor-Transistor Logic), logika '1' mungkin diwakili oleh tegangan sekitar +5 volt, sedangkan logika '0' oleh sekitar 0 volt. Perubahan antara dua logic state ini membentuk informasi yang diproses oleh sirkuit digital, menjadi dasar bagi semua operasi komputasi dan kontrol.
- LOGICPROBE
Untuk memverifikasi atau memecahkan masalah logic state dalam sirkuit, digunakan alat yang disebut logic probe. Sebuah logic probe adalah perangkat uji genggam berbiaya rendah yang dirancang khusus untuk menganalisis dan menampilkan logic state (boolean 0 atau 1) dari suatu titik dalam sirkuit digital. Umumnya, logic probe dilengkapi dengan beberapa indikator LED (Light Emitting Diode): satu LED (seringkali merah) untuk menunjukkan logic high (1), satu lagi (seringkali hijau) untuk logic low (0), dan terkadang LED ketiga (misalnya kuning atau oranye) yang menyala atau berkedip untuk menunjukkan adanya pulsa atau sinyal yang berosilasi. Beberapa logic probe yang lebih canggih bahkan dapat mendeteksi pulsa yang sangat singkat dan menyimpannya (pulse stretching) agar dapat terlihat, serta membedakan antara logic low dan kondisi tri-state (impedansi tinggi atau tidak terhubung) di mana tidak ada level logika yang jelas. Dengan menempelkan ujung probe ke titik tertentu di sirkuit, seorang teknisi dapat dengan cepat menentukan apakah sinyal pada titik tersebut berada dalam state logika yang benar sesuai dengan desain sirkuit.
- AND-GATE
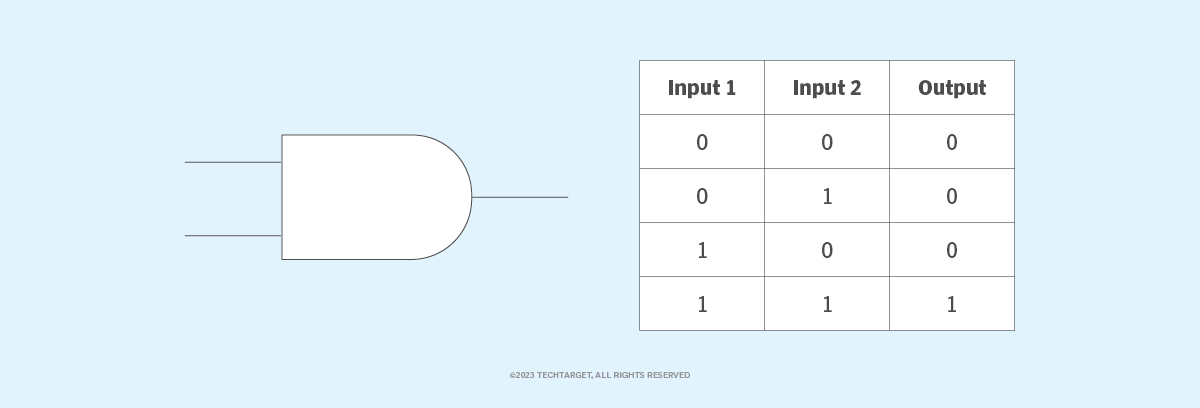
Gerbang AND menghasilkan keluaran benar hanya jika kedua masukan bernilai benar. Jika tidak, keluarannya salah. Dengan kata lain, keluarannya bernilai 1 hanya jika kedua masukan bernilai 1, dan 0 jika salah satu masukan bernilai 0. Gerbang ini dinamai demikian karena, jika 0 salah dan 1 benar, gerbang tersebut bekerja dengan cara yang sama seperti operator logika dan. Gambar 1 menunjukkan tabel kebenaran yang menunjukkan simbol rangkaian dan kombinasi logika untuk gerbang AND. Dalam simbol tersebut, terminal masukan berada di sebelah kiri, dan terminal keluaran berada di sebelah kanan.
- OR-GATE
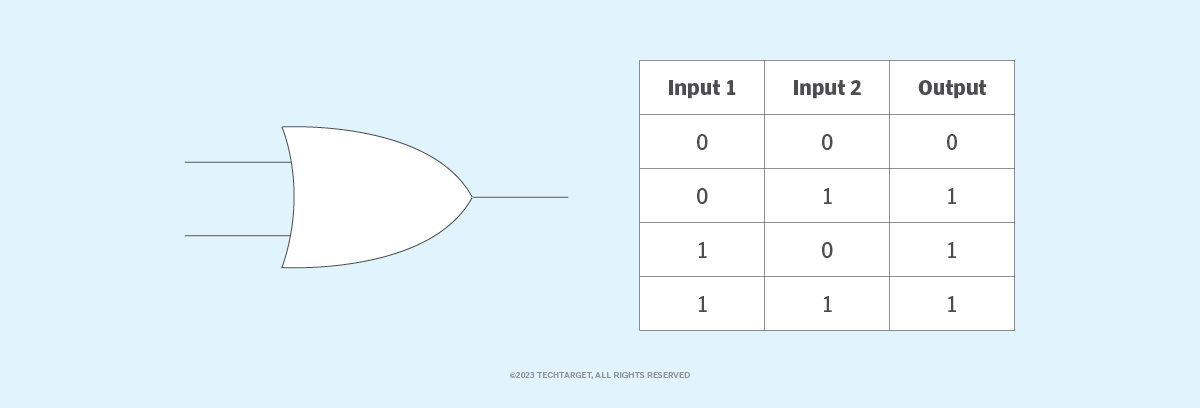
Pada gerbang OR, yang merupakan salah satu rangkaian logika yang paling banyak digunakan dalam perangkat dan komponen digital, keluarannya bernilai benar jika salah satu atau kedua masukan bernilai benar. Jika kedua masukan bernilai salah, keluarannya juga salah. Agar keluarannya bernilai 1, setidaknya satu masukan harus bernilai 1. Gerbang ini mendapatkan namanya karena berperilaku seperti gerbang logika inklusif atau. Gambar 2 menunjukkan tabel kebenaran untuk gerbang OR.
- NOT-GATE
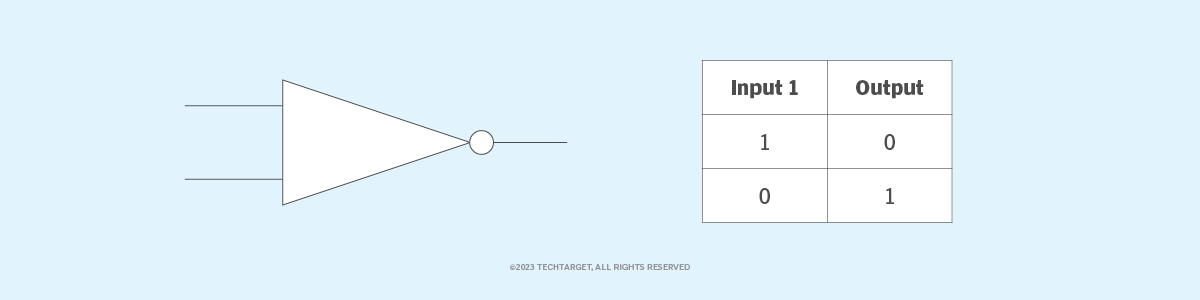
Inverter logika, terkadang disebut gerbang NOT untuk membedakannya dari jenis perangkat inverter elektronik lainnya, hanya memiliki satu masukan. Gerbang NOT membalikkan keadaan logika. Jika masukan gerbang adalah 1, maka keluarannya adalah 0. Jika masukannya 0, maka keluarannya adalah 1. Sebagai salah satu gerbang logika yang menerima satu masukan dan menghasilkan satu keluaran, gerbang NOT juga merupakan salah satu yang paling sederhana karena hanya membalikkan masukan yang diberikan. Seperti ditunjukkan pada Gambar 4, tabel kebenaran untuk gerbang NOT sederhana.
HALF ADDER
Half-adder adalah blok rangkaian aritmatika yang dapat digunakan untuk menjumlahkan dua bit. Rangkaian ini memiliki dua masukan yang mewakili dua bit yang akan dijumlahkan dan dua keluaran, dengan satu keluaran menghasilkan keluaran SUM dan keluaran lainnya menghasilkan keluaran CARRY. Gambar 7.4 menunjukkan tabel kebenaran half-adder, yang menunjukkan semua kemungkinan kombinasi masukan dan keluaran yang sesuai.
Pemeriksaan kedua ekspresi tersebut menunjukkan bahwa tidak ada ruang untuk penyederhanaan lebih lanjut. Ekspresi pertama yang mewakili keluaran SUM adalah gerbang EX-OR, sedangkan ekspresi kedua yang mewakili keluaran SUM adalah gerbang EX-OR.
Keluaran CARRY adalah keluaran gerbang AND. Namun, kedua ekspresi ini tentu dapat direpresentasikan dalam berbagai bentuk menggunakan berbagai hukum dan teorema aljabar Boolean untuk menggambarkan fleksibilitas yang dimiliki perancang dalam mengimplementasikan fungsi kombinasional sesederhana fungsi setengah penjumlah pada perangkat keras. Kita telah mempelajari di Bab 6 tentang aljabar Boolean bagaimana berbagai gerbang logika dapat diimplementasikan dalam bentuk gerbang NAND saja atau gerbang NOR. Meskipun cara paling sederhana untuk mengimplementasikan setengah penjumlah pada perangkat keras adalah dengan menggunakan gerbang EX-OR dua masukan untuk keluaran SUM dan gerbang AND dua masukan untuk keluaran CARRY, seperti yang ditunjukkan pada Gambar 7.5, hal ini juga dapat diimplementasikan dengan menggunakan susunan gerbang NAND atau NOR yang tepat. Gambar 7.6 menunjukkan implementasi setengah penjumlah dengan gerbang NAND saja. Pengamatan lebih dekat pada diagram logika Gambar 7.6 menunjukkan bahwa salah satu bagian rangkaian mengimplementasikan gerbang EX-OR dua masukan dengan gerbang NAND dua masukan. Implementasi EX-OR menggunakan NAND telah dibahas pada bab sebelumnya. Gerbang AND yang diperlukan untuk menghasilkan keluaran CARRY diimplementasikan dengan melengkapi keluaran NAND yang sudah tersedia dari variabel masukan.
FULL ADDER
Rangkaian penjumlah penuh adalah blok rangkaian aritmatika yang dapat digunakan untuk menjumlahkan tiga bit untuk menghasilkan keluaran SUM dan CARRY. Blok penyusun seperti ini menjadi suatu keharusan ketika menjumlahkan bilangan biner dengan jumlah bit yang besar. Rangkaian penjumlah penuh mengatasi keterbatasan penjumlah setengah, yang hanya dapat digunakan untuk menjumlahkan dua bit. Mari kita ingat kembali prosedur penjumlahan bilangan biner yang lebih besar. Kita mulai dengan penjumlahan LSB dari kedua bilangan tersebut. Kita mencatat hasil penjumlahan di bawah kolom LSB dan membawa carry, jika ada, ke bit-bit kolom yang lebih tinggi berikutnya. Akibatnya, ketika kita menjumlahkan bit-bit kolom yang lebih tinggi berikutnya yang berdekatan, kita akan diminta untuk menjumlahkan tiga bit jika terdapat carry dari penjumlahan sebelumnya. Kita memiliki situasi yang serupa untuk bit-bit kolom yang lebih tinggi lainnya.
Penjumlah penuh dari jenis yang dijelaskan di atas membentuk blok dasar penjumlah biner. Namun, satu rangkaian penjumlah penuh hanya dapat digunakan untuk menjumlahkan bilangan biner satu bit. Susunan kaskade penjumlah ini dapat digunakan untuk membangun penjumlah yang mampu menjumlahkan bilangan biner dengan jumlah bit yang lebih besar. Misalnya, penjumlah biner empat bit akan membutuhkan empat penjumlah penuh dari jenis yang ditunjukkan pada Gambar 7.10 untuk dihubungkan secara kaskade. Gambar 7.11 menunjukkan susunan tersebut. (A3A2A1A0 dan (B3B2B1B0) adalah dua bilangan biner yang akan dijumlahkan, dengan A0 dan B0 mewakili LSB dan A3 dan B3 mewakili MSB dari kedua bilangan tersebut.
HALF SUBSTRACTOR
Setengah pengurang adalah rangkaian kombinasional yang dapat digunakan untuk mengurangkan satu digit biner dari digit lainnya untuk menghasilkan keluaran DIFFERENCE dan keluaran BORROW. Keluaran BORROW di sini menentukan apakah angka '1' telah dipinjam untuk melakukan pengurangan. Tabel kebenaran setengah pengurang, seperti yang ditunjukkan pada Gambar 7.12, menjelaskan hal ini lebih lanjut. Ekspresi Boolean untuk kedua keluaran tersebut diberikan oleh persamaan.
gerbang EX-OR, ekspresi untuk keluaran BORROW (Bo adalah gerbang AND dengan masukan A yang dikomplemen sebelum dimasukkan ke gerbang. Gambar 7.13 memperlihatkan implementasi logika setengah-pengurang. Dengan membandingkan setengah-pengurang dengan setengah-penjumlah, kita menemukan bahwa ekspresi untuk keluaran SUM dan DIFFERENCE sama saja. Ekspresi untuk BORROW dalam kasus setengah-pengurang juga mirip dengan apa yang kita miliki untuk CARRY dalam kasus setengah-penjumlah. Jika masukan A, yaitu, yang dikurangi, dikomplemen, gerbang AND dapat digunakan untuk mengimplementasikan keluaran BORROW. Perhatikan kesamaan antara diagram logika pada Gambar 7.5 (setengah-penjumlah) dan Gambar 7.13 (setengah-pengurang).
FULL SUSTRACTOR
Pengurang penuh melakukan operasi pengurangan pada dua bit, sebuah minuend dan sebuah pengurang, dan juga mempertimbangkan apakah bit '1' telah dipinjam oleh bit minuend bawah yang berdekatan sebelumnya atau belum. Akibatnya, ada tiga bit yang harus ditangani pada masukan pengurang penuh, yaitu dua bit yang akan dikurangi dan sebuah bit peminjam yang ditetapkan sebagai Bin. Ada dua keluaran, yaitu keluaran DIFFERENCE D dan keluaran BORROW. Bit keluaran BORROW memberi tahu apakah bit minuend perlu meminjam '1' dari bit minuend yang lebih tinggi berikutnya. Gambar 7.14 menunjukkan tabel kebenaran pengurang penuh.
Jika kita membandingkan ekspresi-ekspresi ini dengan ekspresi yang diturunkan sebelumnya dalam kasus penjumlahan penuh, kita menemukan bahwa ekspresi untuk keluaran DIFFERENCE D sama dengan ekspresi untuk keluaran SUM. Selain itu, ekspresi untuk keluaran BORROW mirip dengan ekspresi untuk CARRY-OUT Co.
Figure 7.26
- Siapkan semua komponen yang dibutuhkan : LOGISTATE, LOGICPROBE, SISTEM (AND-GATE, OR-GATE, DAN NOT)
- Buat sistem HA, lalu masuk ke CHILD SHEET-nya. Rangkailah rangkaian half adder di dalamnya dengan input A, B dan output S.
- Buat sistem HS, lalu masuk ke CHILD SHEET-nya. Rangkailah rangkaian half substractor di dalamnya dengan input S, C dan output D, B.
- Susun rangkaian sesuai dengan gambar : LOGICSTATE > HA > HS > LOGICPROBE
- Simulasikan rangkaian dengan menekan tombol PLAY.
Figure 7.27
- Siapkan semua komponen yang dibutuhkan : LOGISTATE, LOGICPROBE, XOR-GATE, dan IC7483 (4-bit Full Adder)
- Susun rangkaian sesuai dengan gambar : LOGICSTATE > XOR-GATE > IC7483 > LOGICPROBE
- Simulasikan rangkaian dengan menekan tombol PLAY.
RANGKAIAN SIMULASI & PRINSIP KERJANYA
Fig 7.26
Prinsip kerja rangkaian pada gambar ini adalah untuk merepresentasikan operasi pengurangan biner menggunakan kombinasi dua rangkaian dasar: Half Adder (HA) dan Half Subtractor (HS). Half Adder (HA) pada dasarnya digunakan untuk menghasilkan penjumlahan (SUM) dan carry-out dari dua input biner. Output dari HA ini kemudian diumpankan ke rangkaian Half Subtractor (HS) bersama dengan input biner ketiga (C). Half Subtractor (HS) bertanggung jawab untuk menghasilkan selisih (DIFFERENCE) dan pinjaman (BORROW). Dengan demikian, keseluruhan rangkaian berfungsi sebagai "Full Subtractor" yang dapat mengurangi tiga bit input, di mana HA mengurus sebagian dari operasi penjumlahan/pengurangan awal, dan HS menyelesaikan operasi pengurangan untuk mendapatkan selisih akhir dan bit pinjaman. Tabel kebenaran yang disertakan menunjukkan bagaimana kombinasi input A, B, dan C menghasilkan output DIFFERENCE dan BORROW yang sesuai, memvalidasi fungsi rangkaian sebagai pengurang biner.
Fig. 7.27
Prinsip kerja rangkaian ini adalah untuk melakukan operasi penjumlahan atau pengurangan biner delapan bit pada dua bilangan biner (A dan B) berdasarkan sinyal kontrol "OPERATOR". Rangkaian ini mengimplementasikan sebuah adder/subtractor menggunakan dua chip IC 74LS83, yang merupakan 4-bit binary adder lengkap dengan carry-in dan carry-out, dikombinasikan dengan gerbang XOR (74LS86) dan dip switch sebagai input. Ketika sinyal "OPERATOR" (control input) bernilai 0, gerbang XOR akan meneruskan bit B apa adanya ke input carry-in adder dan input B pada adder, sehingga rangkaian berfungsi sebagai adder (penjumlahan A+B). Namun, ketika sinyal "OPERATOR" bernilai 1, gerbang XOR akan menginversi setiap bit dari bilangan B sebelum diumpankan ke adder, mengubahnya menjadi komplemen satu (1's complement) dari B; pada saat yang sama, carry-in pada adder pertama juga diatur ke 1, yang secara efektif mengubah operasi penjumlahan menjadi pengurangan dengan menggunakan metode komplemen dua (2's complement) (yaitu, A + (2's complement B) = A - B). Dengan demikian, rangkaian ini secara fleksibel dapat melakukan operasi penjumlahan atau pengurangan pada bilangan biner 8-bit hanya dengan mengubah satu sinyal kontrol.
6. FILE DOWNLOAD [Back]
Berikut ini adalah file Proteus terkait:
- Download 7.26 klik disini
- Download 7.27 klik disini
Berikut ini adalah datasheet terkait:
- Download HA klik disini
- Download HS klik disini










Komentar
Posting Komentar